Con una destacada participación, estudiantes de la carrera de Ingeniería Matemática de la Universidad de Santiago de Chile (USACH), perteneciente al Departamento de Matemática y Ciencia de la Computación (DMCC), presentaron sus trabajos de investigación en el Encuentro Nacional de Ingeniería Matemática 2025 (ENIM 2025), realizado entre el martes 17 y el viernes 19 de diciembre en la Universidad de Concepción.
El evento, organizado por estudiantes del plan de Ingeniería Matemática de la casa de estudios penquista, tuvo como objetivo fortalecer el intercambio académico y humano, además de promover la vinculación entre estudiantes, académicos y empresas, abarcando diversas áreas de la matemática teórica y aplicada.
Durante las tres jornadas, cerca de doscientos estudiantes provenientes de nueve universidades del país participaron en cursos especializados dictados por investigadores, charlas académicas sobre temáticas de frontera, mesas de discusión en torno a los desafíos actuales de la disciplina y presentaciones de resultados de investigación desarrollados por estudiantes.
En este contexto, la delegación de nuestra universidad presentó tres trabajos en formato póster, reflejando el compromiso de sus estudiantes con la investigación temprana y el acompañamiento activo de sus profesores, así como el apoyo institucional de la Facultad de Ciencia.
- Modelación de incendios forestales mediante inteligencia artificial:
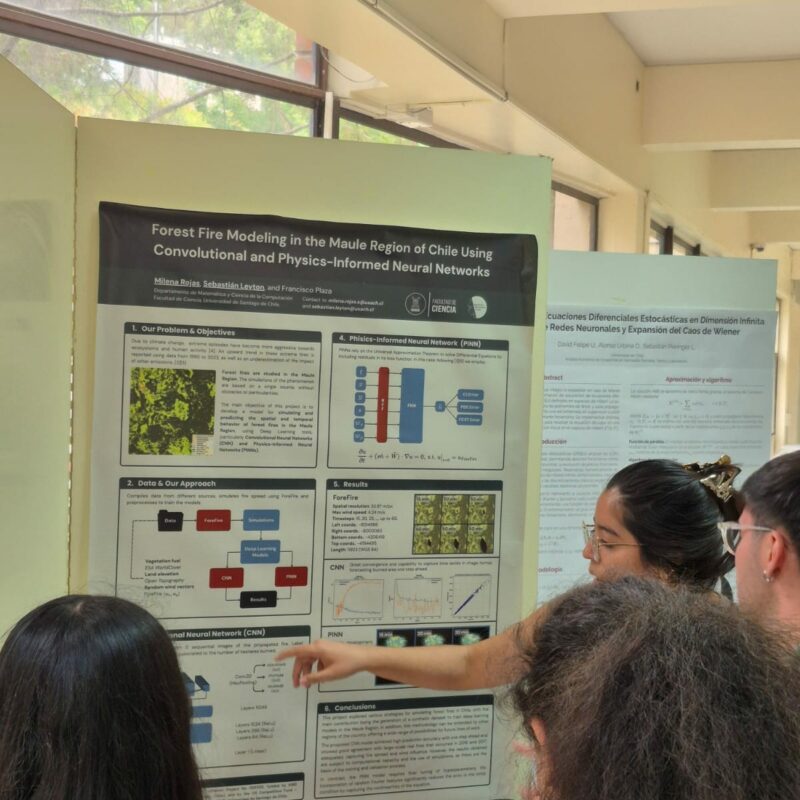
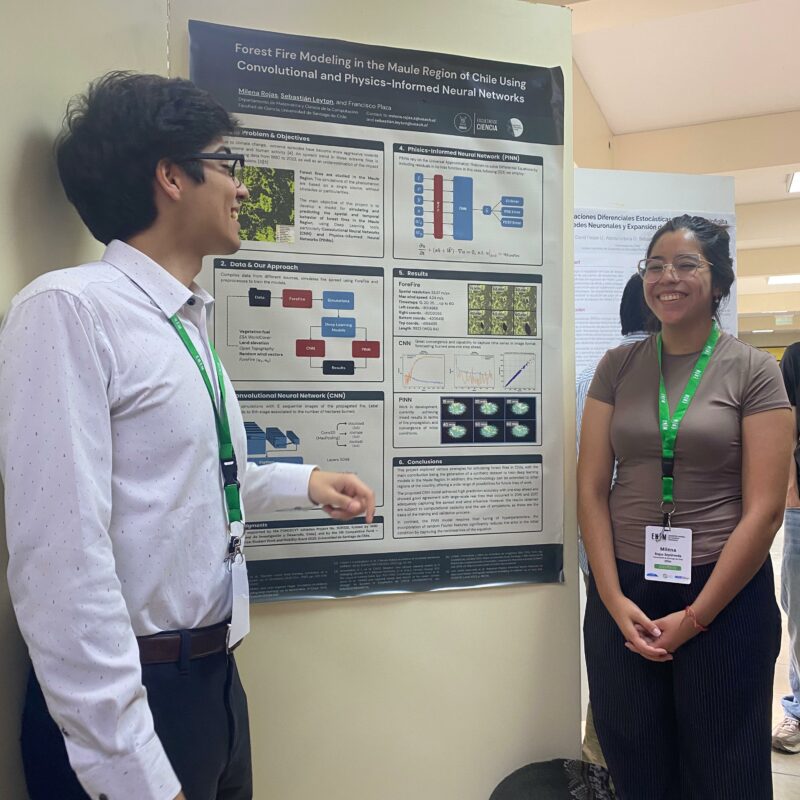
- El trabajo “Forest Fire Modeling in the Maule Region of Chile Using Convolutional and Physics-Informed Neural Networks”, presentado por Milena Rojas y Sebastián Leyton, junto al académico Francisco Plaza Vega, aborda una problemática de alto impacto social y ambiental: los incendios forestales en Chile. La investigación se enmarca en un proyecto de Fondos Concursables del fondo VIME de la Facultad de Ciencia, orientado a fomentar la investigación conjunta entre estudiantes y profesores, y además cuenta con el respaldo del Proyecto FONDECYT de Iniciación N°11251120 (2025), titulado “Climate Change: Spatio-Temporal Ecosystem-Based Dynamics Using Statistical Tools, Generative AI, and Long-Memory Time Series”, a cargo del profesor Plaza Vega. El estudio propone el uso de redes neuronales convolucionales y redes neuronales informadas por física para simular incendios forestales en la Región del Maule, integrando información de vegetación, topografía y condiciones meteorológicas, con el objetivo de avanzar hacia herramientas que permitan comprender y anticipar eventos extremos asociados al cambio climático.
- Modelos estocásticos para el estudio de dinámicas poblacionales:
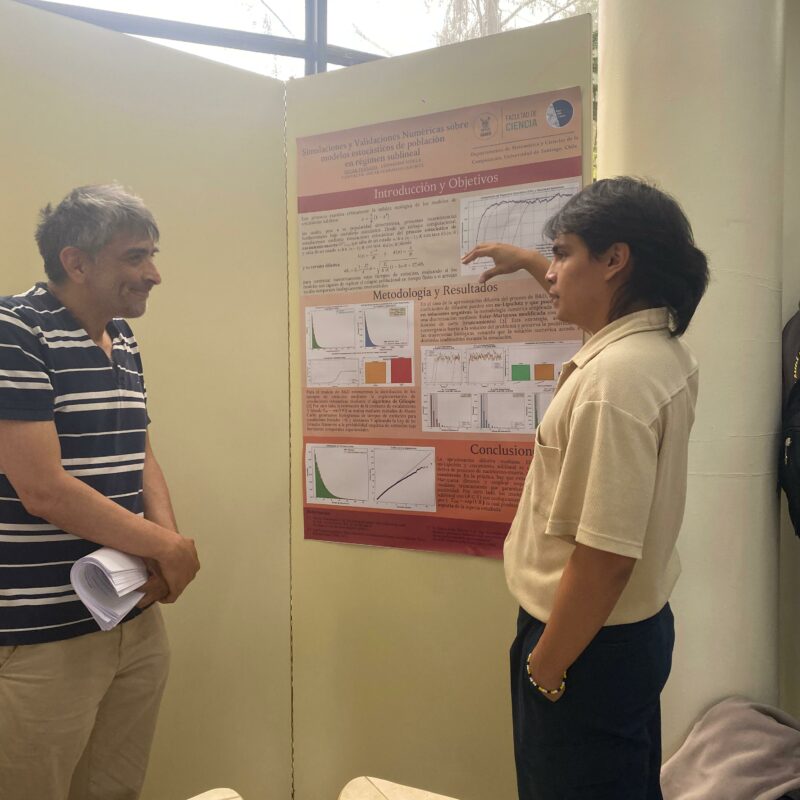
- Por su parte, Oscar Ferrada, junto al académico Leonardo Videla, presentó el trabajo “Simulaciones y Validaciones Numéricas sobre modelos estocásticos de población en régimen sublineal”, enfocado en el análisis de procesos estocásticos aplicados a modelos de crecimiento poblacional. Esta investigación se desarrolló en el marco de un proyecto de Fondos Concursables de la Facultad de Ciencia, adjudicado al estudiante durante el segundo semestre, y combina simulaciones computacionales con resultados teóricos recientes para estudiar tiempos de extinción, escalas de crecimiento y estabilidad en poblaciones finitas. El trabajo aporta un enfoque cuantitativo y reproducible para el estudio de riesgos de extinción en sistemas biológicos.
- Persistencia estocástica y genética de poblaciones:
- El tercer póster presentado correspondió a “Persistencia Estocástica en Cadenas de Markov No Lineales: Aplicación a modelos de genética de poblaciones”, desarrollado por Astrid Grassau junto al profesor Leonardo Videla. Este trabajo se enmarca dentro de las actividades del Seminario de Título II de la estudiante y cuenta con financiamiento parcial del Proyecto FONDECYT de Iniciación N°11240158 (2024), titulado “Adaptive behavior in stochastic population dynamics and non-linear Markov processes in ecoevolutionary modeling”, a cargo del profesor Videla. La investigación aborda modelos estocásticos avanzados para estudiar la persistencia de poblaciones, combinando cadenas de Markov no lineales y ecuaciones de tipo McKean–Vlasov aplicadas a genética de poblaciones.
Formación, vinculación y proyección académica
Los estudiantes que participaron en este encuentro, destacaron el ENIM 2025 como una instancia clave para compartir con pares de otras universidades, intercambiar experiencias y reforzar la confianza en el trabajo que se desarrolla en la USACH. Asimismo, valoraron la oportunidad de presentar resultados propios, introducirse tempranamente en el mundo de la investigación y despertar el interés de futuros colegas.
Finalmente, agradecieron el apoyo del Departamento de Matemática y Ciencia de la Computación y de la Facultad de Ciencia, así como el acompañamiento de los académicos involucrados, destacando que este tipo de iniciativas fortalecen su formación profesional y consolidan el rol de la USACH como un espacio activo en investigación y desarrollo en matemática teórica y aplicada.